9.C Intervallumok: házik

Sep 27, 2019Sep 27, 2019 / halaszi

Legyenek hétfőre az alábbiak:

Jpeg

Kérlek, oszd be, naponta egyet-kettőt csinálj meg.

Mat. I., 3. gyakorlat; az első elméleti zárthelyi eredményei

Sep 26, 2019Sep 26, 2019 / halaszi

3.gyakorlat_mat_I_halasz_19-20

A házi feladatok:

az előző, 2. feladatsorból 7. b), d)
az aktuális, 3.-ból 1. a), d), g), i), l); 2. mindegyik függvénye

Jpeg

Az első elméleti zárthelyin elért eredmények a maximális 12 pontból:

neptun	pontszám
DCC…	12
HZO…	11
T5H…	2
RJQ…	10
AJG…	12
OZU…	10
QFV…	8
C78…	11
HAQ…	6
QVF…	8
CCZ…	12
II1…	5
H77…	5
O7V…	11
SB4…	11
F80…	5
WTB…	10
NKU…	5
V4S…	11
AS2…	7
H92…	7
CQQ…	11
E9Z	8
BFM…	7
JLE…	10
VQ0…	4
P8T…	5
G4S…	9

7.A Öles törtesek

Sep 26, 2019 / halaszi

Szigorúan napi egyet hétfőig (még ma végezd el az órai utolsót, aztán holnaptól):

Jpeg

9.A Fizikaházik az egyenletes mozgásra

Sep 20, 2019 / halaszi

Tekintsük a haj átlagos növekedési sebességét 20 centiméternek évente. Mennyit nő (a) egy nap, (b) egy hét, (c) egy hónap, (d) egy másodperc alatt?
Egy gépkocsi egyenletesen halad az egyenes országúton. Az utasok 10 perc alatt 13 kilométerkövet számolnak meg. (a) Hány m/s a gépkocsi sebessége? (b) Mennyit mutat a kilométerórája?
Palackozó gépsorról percenként 80 üveg kerül le. Az üvegek összeérnek és két üveg 39 cm helyet foglal el. Milyen sebességgel halad a futószalag?
Egy vízmelegítő percenként 9,6 dm³ vizet enged át. Hány m/s sebességgel folyik a víz a 2 cm² keresztmetszetű csapból?

12.C Mozgókép & hang, Carson, Popper

Sep 20, 2019 / halaszi

A filmet elérheted az office-fiókodban, megosztottam veled a OneDrive-on. Ha kell, van felirat is a mappában; az ofisz lejátszója nem csatolja magától, találj ki vmit.
A szövegértésihez, a környezetvédelemhez: Rachel Carson
Popper bácsitól egy lehetséges választás:

12.C Szövegértés péntekre. Uncivil War

Sep 18, 2019 / halaszi

Péntekre, kérlek: szövért_fenntarthat

A holnapi Brexit filmhez felvezetésül:

9.C Szimmetrikus differencia. Házik

Sep 18, 2019 / halaszi

Halmazok szimmetrikus differenciája

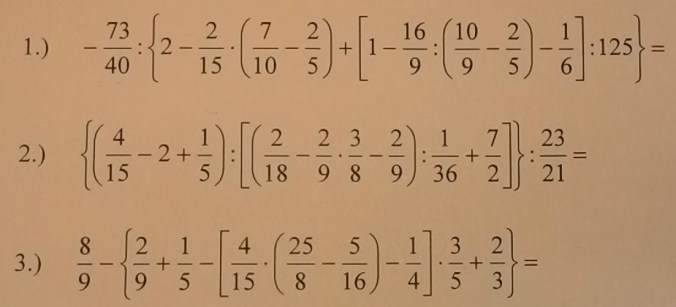
Az A és B halmaz szimmetrikus differenciáján azon elemek halmazát értjük, amelyek csak az egyiknek (pontosan az egyiknek) elemei.

A Δ B = (A \ B) ∪ (B \ A)

Logikailag ez a kizáró vagy (eXclusive OR, azaz a XOR) művelet. A megengedő vagy az unióé.

Hasznos megfogalmazása a következő is:

A Δ B = (A ∪ B) \ (A ∩ B).

Kérlek, oldd meg a következő feladatlap 1., 3., 9., 16. és 18. feladatát: SG_Halmazok

12.C Összehasonlító elemzés

Sep 17, 2019Sep 17, 2019 / halaszi

Szerdára (holnap, 09.18.) várom a vázlatot az összehasonlító elemzés szempontjaival és a megállapításokkal, amikből jövő hétfőre várom a kész értekezést.

bordal; Vörösmarty vs. Petőfi

9.C Halmazműveletek

Sep 17, 2019 / halaszi

A szerdai (szept. 18-i) óránkra az alábbi fotóról: 1. e), h), 4. első oszlopa (a), e), i), m)), 5.

Jpeg

Mat. I., 2. gyakorlat

Sep 16, 2019 / halaszi

Az 1. gyakorlat feladatsorából kérem szeptember 23-ra még az 5-10. és a 12. feladatot; valamint az alábbi, 2. feladatsorból az 1. c), d), f), g)-t illetve a 3. b)-t.

2.gyakorlat_mat_I_halasz_19-20

Az esedékes (09. 23.) elméleti kis zéhában az első két előadás és gyakorlat alapvető fogalmai és tételei szerepelnek majd kimondásuk és elemi alkalmazásuk szintjén.

A 2. gyakorlaton történtek:

Jpeg